Analysis of different implementation of multiplier, summarize from SoC(MST3319) and CA(MST3305)

Multiplier

Focus

• optimize signed multiplier(which is usually more complex than unsigned multiplier)
• encode compressor/optimize(booth recoding, baugh-wooley)
• full adder tree compression(wallace tree, dadda tree)

2 tradeoff ideas

• in CA class, take 32 * 32 for example, multiplier introduced is achieved with a 64 bit reg for result storage, initialized with 32 bit multiplier at its lower 32 bit. a controller, a shifter, a 64 bit adder. It takes more cycles to calculate the output, but it occupies less area and can achieve higher frequency.

• in SoC class, multiplier is achieved as a pure combinational logic, mainly composed of CSA tree(carry store adder) or HA/FA array, organizing in a tree structure. It takes larger area, but it cosumes a single cycle to produce the result.

Implementation

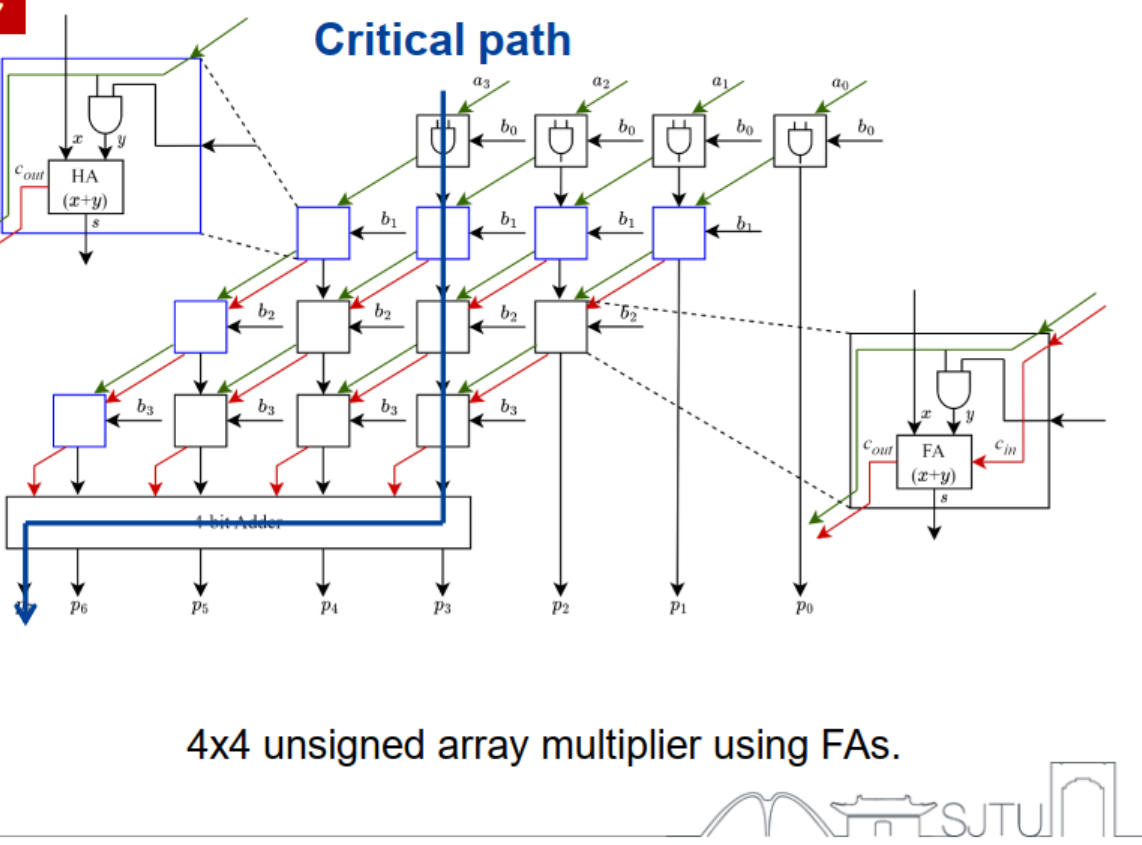
take 4 * 4 unsigned multiplier for example

First unroll the multiplication to adder tree form

naive implementation

implement multiplier in the form of adder array, composed of FA/HA, in the shape of four level adder tree with each level of a bit of shift

wallace tree compressor

At first level, compress the four level adder tree composed of partial product with half adder or carry store adder, generate stored carry out bit and sum bit. (for 4 * 4 here, with a level of carry store adder or half adder, the height of adder tree can be compressed from 4 to 2, in fact 3+1 to 2+1), at second level the height of adder tree be compressed to 2, then feed them into 4 bit full adder to generate the final product

for signed 4 * 4 multiplier with wallace tree compressor, at partial product generation stage, each partial product should be sign extended to 8 bit, and then carry out compression, so it consumes more hardware area(but the the height of adder tree is still the same)

booth recoding

optimize for signed multiplication

product generation

take radix-2 4 * 4 unsigned multiplication for example, booth recoding can compress the height of product adder tree from 4 to 3(radix-4, radix-8 compress more, but recoding hardware takes area)

sign extension in partial product generation

baugh-wooley